Hückelovo pravidlo
2. 2. 2007
Jméno Ericha Hückela, německého vědce narozeného ve Stuttgartu roku 1896, je mezi chemiky velmi dobře známo. Je totiž autorem pravidla (podmínky), které patří mezi kritéria, jež rozhodují o tom, zda-li je daná sloučenina aromatická, či nikoliv.
Aby byla daná latka aromatická, musí být molekula planární, monocyklická, mít dokonale konjugovaný systém vazeb a splňovat právě onu Hückelovu podmínku. Ta říká, že počet pí-elektronů ve sloučenině musí být roven číslu 4n+2, tedy matematicky P= 4n+2, kde P je počet pí-elektronů a n je libovolné celé nezáporné číslo.
Ovšem proč zrovna 4n+2??? Co je na této kombinaci tak speciálního? Proč tedy zrovna 2, 6, 10, 14... pí-elektronů vede k aromaticitě a poměrně vysoké stabilitě, zatímco ostatní kombinace vedou k větší či menší nestabilitě. Odpověď se skrývá v "tajemné" teorii molekulových orbitalů (MO).
Pokud se totiž spočítají energetické hladiny molekulových orbitalů pro cyklické konjugované molekuly, ukáže se, že vždy existuje jeden nejníže ležící MO, nad kterým existují MO v degenerovaných párech. Tedy, při zaplňováníí MO je vždy potřeba dvou elektronů na zaplnění nejníže ležícího osamoceného MO a poté vždy čtyř elektronů na zaplnění každé z n následujících energetických hladin - dohromady tedy 2 + 4n. Každý jiný počet zanechá energetickou hladinu částečně nezaplněnou a tedy méně stabilní.
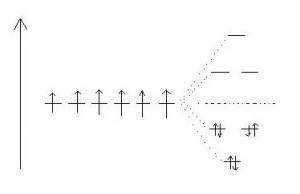
OBR: Molekulové orbitaly pro benzen:
1. Šipka vlevo ukazuje růst energie systému
2. Šest nedegenerovaných 2p atomových orbitalů (AO) šesti atomů uhlíku v cyklu benzenu s jedním elektronem v každém z nich
3. Při konjugaci a vzniku molekulových orbitalů vznikají tři vazebné MO o nižší energii než měly puvodní AO (dva jsou degenerované) a tři protivazebné MO o vyšší energii než měly původní AO (dva jsou opět degenerované)
4. Vazebné MO jsou zaplněny elektrony - je vidět, proč jich musí být právě 4n + 2 - tak dojde k zaplnění všech vazebných MO, kdyby jich byl jiný počet, některá místa by byla zbytečně volná.
Aby byla daná latka aromatická, musí být molekula planární, monocyklická, mít dokonale konjugovaný systém vazeb a splňovat právě onu Hückelovu podmínku. Ta říká, že počet pí-elektronů ve sloučenině musí být roven číslu 4n+2, tedy matematicky P= 4n+2, kde P je počet pí-elektronů a n je libovolné celé nezáporné číslo.
Ovšem proč zrovna 4n+2??? Co je na této kombinaci tak speciálního? Proč tedy zrovna 2, 6, 10, 14... pí-elektronů vede k aromaticitě a poměrně vysoké stabilitě, zatímco ostatní kombinace vedou k větší či menší nestabilitě. Odpověď se skrývá v "tajemné" teorii molekulových orbitalů (MO).
Pokud se totiž spočítají energetické hladiny molekulových orbitalů pro cyklické konjugované molekuly, ukáže se, že vždy existuje jeden nejníže ležící MO, nad kterým existují MO v degenerovaných párech. Tedy, při zaplňováníí MO je vždy potřeba dvou elektronů na zaplnění nejníže ležícího osamoceného MO a poté vždy čtyř elektronů na zaplnění každé z n následujících energetických hladin - dohromady tedy 2 + 4n. Každý jiný počet zanechá energetickou hladinu částečně nezaplněnou a tedy méně stabilní.

OBR: Molekulové orbitaly pro benzen:
1. Šipka vlevo ukazuje růst energie systému
2. Šest nedegenerovaných 2p atomových orbitalů (AO) šesti atomů uhlíku v cyklu benzenu s jedním elektronem v každém z nich
3. Při konjugaci a vzniku molekulových orbitalů vznikají tři vazebné MO o nižší energii než měly puvodní AO (dva jsou degenerované) a tři protivazebné MO o vyšší energii než měly původní AO (dva jsou opět degenerované)
4. Vazebné MO jsou zaplněny elektrony - je vidět, proč jich musí být právě 4n + 2 - tak dojde k zaplnění všech vazebných MO, kdyby jich byl jiný počet, některá místa by byla zbytečně volná.
Komentáře
Přehled komentářů
Zatím nebyl vložen žádný komentář